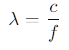Magnitudes Físicas del Sonido

El sonido es un fenómeno complejo que combina aspectos físicos, perceptivos y técnicos. Para poder describirlo con precisión, se suelen emplear una serie de magnitudes físicas del sonido que permiten cuantificar sus características esenciales: presión, intensidad, potencia, velocidad, frecuencia, etc.

Este artículo presenta una exposición rigurosa de las principales magnitudes del sonido, su definición, su relación mutua y su relevancia práctica en grabación, acústica y audio profesional. Verás cómo esas magnitudes físicas no sólo se definen matemáticamente, sino que tienen implicaciones directas en decisiones de diseño de sistemas de audio, medición acústica y producción sonora.

1. Concepto de magnitudes físicas del sonido

Cuando hablamos de «magnitudes del sonido», nos referimos a cantidades físicas cuantificables que describen el comportamiento de una onda sonora. No se trata de “sensaciones” , sino de propiedades medibles del medio y la onda.

Veamos a continuación las más importantes.

2. Frecuencia y periodo

Frecuencia (f)

La frecuencia es la cantidad de oscilaciones por segundo de la onda sonora, y se mide en hertz (Hz).

Matemáticamente, es:

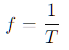
donde T es el período (tiempo que tarda una oscilación completa).

f es la frecuencia está directamente relacionada con la altura tonal (pitch): a mayor frecuencia, más agudo el sonido.

Periodo (T)

El periodo es el tiempo que tarda la onda en completar un ciclo. Se expresa en segundos (s). Es el inverso de la frecuencia:

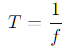
donde T es el período (tiempo que tarda una oscilación completa).

f es la frecuencia está directamente relacionada con la altura tonal (pitch): a mayor frecuencia, más agudo el sonido.

Longitud de onda (λ)

La longitud de onda es la distancia física que ocupa una oscilación completa en el medio (por ejemplo, en el aire). Relaciona la velocidad del sonido (c) con la frecuencia (f):

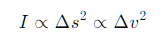
Aquí, c es la velocidad de propagación del sonido en ese medio (por ejemplo, ~343 m/s en aire a 20 °C).

f es la Frecuencia

3. Amplitud y presión acústica

Amplitud (Δp o presión amplitud)

La amplitud en el contexto acústico se refiere a la magnitud de las variaciones de presión causadas por la onda sonora sobre la presión estática del medio. Es decir, en una onda sonora la presión cambia localmente, comprimiendo y rareficando el medio (aire, agua, etc.). Esa variación máxima se llama amplitud de presión (o “presión acústica”).

Si el nivel de presión es grande, el sonido se percibe más fuerte (más “intenso”).

Matemáticamente, si la presión instantánea es p(t), la amplitud máxima es:

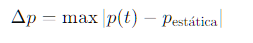
Presión eficaz (rms) y nivel de presión sonora (SPL)

Como el sonido varía con el tiempo, para cuantificarlo se usa el valor RMS (root mean square) de la presión, Prms​. Se define de forma que la energía promedio se relacione con Prms​. Esto es importante porque la intensidad acústica depende de la presión al cuadrado.

El nivel de presión sonora (SPL) se expresa en decibelios (dB) y se calcula así:

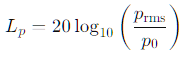
donde p0​ es la presión de referencia (generalmente 20 µPa en aire).

El SPL es una forma conveniente de expresar rangos muy amplios de presión en una escala manejable.

4. Intensidad acústica y potencia

Intensidad acústica (I)

La intensidad acústica (o simplemente intensidad) es la cantidad de energía sonora que atraviesa una unidad de área por unidad de tiempo, en la dirección de propagación de la onda. Se mide en W/m² (vatios por metro cuadrado).

Para una onda senoidal de presión p(t) y velocidad de partícula v(t):

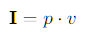
El valor promedio en el tiempo de esta magnitud es el que se usa en práctica.

También se puede expresar el nivel de intensidad sonora en decibelios con respecto a una intensidad de referencia.

Para ondas planas, hay una relación simple entre presión y velocidad usando la impedancia característica del medio (densidad × velocidad acústica) que permite convertir entre presión y intensidad.

Potencia acústica (P)

La potencia acústica es la energía sonora emitida por una fuente por unidad de tiempo, expresada en vatios (W). Es una magnitud de fuente, no localizada como la presión ni la intensidad (estas últimas dependen del punto de medida). Wikipedia+1

Relacionando potencia con intensidad:

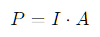
donde A es la superficie a través de la cual se transmite el sonido (por ejemplo, la superficie de una esfera alrededor de la fuente). En propagación esférica, la intensidad decae proporcional a 1/r2

5. Velocidad del sonido

La velocidad del sonido es la rapidez con que una perturbación acústica (frente de onda) se traslada en un medio. Se denota como c y depende de las propiedades del medio (densidad, módulo elástico, temperatura, humedad). En aire a ~20 °C, vale aproximadamente 343 m/s.

La fórmula básica (para un gas ideal) es:

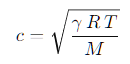
donde γ es el coeficiente adiabático, R es la constante de gas, T es la temperatura absoluta y M la masa molar del gas.

La velocidad del sonido es clave para relacionar longitud de onda y frecuencia, como vimos antes λ=c/f

6. Impedancia acústica

Impedancia acústica específica (z)

La impedancia acústica específica, z, es la relación entre presión y velocidad de partícula:

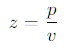
Se mide en Pa·s/m (o N·s/m³). Esta magnitud describe cómo se oponen el medio y la onda al movimiento de partículas.

Impedancia característica del medio (Z₀)

La impedancia característica del medio es:

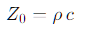
donde ρ es la densidad del medio y c la velocidad del sonido en ese medio. Una onda plana ideal cumple z=Z0

La impedancia resulta fundamental cuando consideramos reflexiones, transmisiones y acoplamientos entre medios (por ejemplo, aire a membrana de un micrófono, filtro acústico, interfaz onda-medio).

7. Relación entre magnitudes

Intensidad vs. presión

Para ondas acústicas planas:

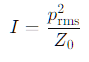
Esto muestra que la intensidad es proporcional al cuadrado de la presión RMS, si la impedancia del medio es constante.

Por lo tanto, duplicar la presión implica cuadruplicar la intensidad (un aumento de +6 dB en nivel de presión produce un aumento de +6 dB en nivel de intensidad).

Decaimiento con la distancia

• La presión sonora para una fuente puntual en propagación esférica decrece como 1/r
• La intensidad acústica disminuye como 1/r2 (por la expansión del frente de onda).

Este comportamiento de decaimiento es parte esencial cuando se diseña sonorización en directo, salas, disposición de altavoces y mediciones acústicas (como en sistemas line array, que asumirán estos principios).

Conversión presión ↔ potencia

Si una fuente emite potencia acústica P de forma isotrópica, la intensidad en una superficie esférica de radio r es:

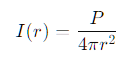
Y la presión RMS asociada en esa superficie, asumiendo onda directa y medio homogéneo:

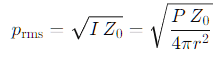
Estas relaciones permiten ir de una magnitud a otra, útiles en cálculos acústicos reales.

8. Otras magnitudes y consideraciones

Nivel acústico (decibelios) y escalas logarítmicas

Como los rangos de presión e intensidad que el oído humano percibe son enormes (de ~20 µPa hasta decenas de Pa), se usa escala logarítmica en decibelios:

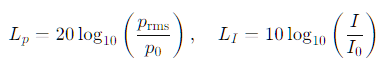
Donde p0=20 μPa = 20 (referencia de presión en aire) y I0 es una intensidad de referencia (~10⁻¹² W/m²)

Este uso de decibelios permite sumar, comparar y mezclar niveles de forma más práctica.

También se aplican ponderaciones (A, C, etc.) para adaptar mediciones a la sensibilidad del oído humano en diferentes frecuencias.

Amplitud de desplazamiento y velocidad de partícula

Aunque la presión es la magnitud más usada, teóricamente también se puede describir la onda sonora en términos de desplazamiento de partículas (Δs) o velocidad de partícula (Δv). La intensidad puede expresarse también mediante esas variables:

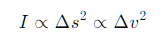
La relación entre Δv y Δs sigue que Δv=2πf Δs

En la práctica, esas magnitudes son más difíciles de medir directamente, por lo que la presión acústica sigue siendo la métrica estándar.

Espectro, contenido armónico y timbre

El espectro de frecuencias de una señal sonora (distribución de amplitud o energía por frecuencia) no es “una magnitud física del sonido” per se, pero es imprescindible para calcular magnitudes físicas en contextos reales (la presión resultante es la suma de componentes en frecuencia).

El timbre es una cualidad perceptiva que surge de esa distribución de armónicos y su envolvente. Aunque no medible directamente como una magnitud física simple, su análisis espectral y la relación entre magnitudes físicas de cada componente es vital.

Absorción, reflexión, transmisión

Cuando una onda sonora incide sobre un medio diferente (pared, membrana, material), parte de la energía se refleja, se transmite o se absorbe. Aparecen coeficientes de absorción y de reflexión, que son proporciones adimensionales (0 a 1) que conectan la energía incidentes con la reflejada o absorbida.

Estas magnitudes forman parte esencial del diseño acústico de salas, cabinas, tratamiento acústico, etc.

9. Aplicaciones prácticas en audio, medición y grabación

Medición en campo y calibración

Para medir magnitudes del sonido en entornos reales (conciertos, salas de ensayo, estudios, instalaciones), se utilizan sonómetros y medidores de nivel de presión sonora (SPL meters) que miden LpL_pLp​. En grabación y sonido directo, entender el nivel de presión esperado en el escenario es clave para escoger micrófonos, colocaciones y niveles de referencia.

La conversión entre presión e intensidad es útil cuando se trabaja con arrays de micrófonos de intensidad o sondas de intensidad, que captan presión y gradiente para calcular vectores de intensidad sonora.

Diseño de sistemas de sonido

En sistemas PA, altavoces, arrays, es crucial prever la distribución de presión en la audiencia, el decaimiento con la distancia y la potencia requerida. Los principios de que la presión decae como 1/r1/r1/r e intensidad como 1/r21/r^21/r2 son fundamentales al dimensionar amplificación, angulación, niveles, cobertura.

Además, la impedancia acústica del aire y el acoplamiento con bafles, difusores y filtros (corto de graves, hornos, etc.) usan el concepto de impedancia acústica para optimizar transferencia de energía.

Grabación y mezcla

Al capturar sonido con micrófonos, la presión acústica es la magnitud capturada (convertida en voltaje). La elección de micrófono, sensibilidad, SPL máximo admisible, distorsión, etc., están todas condicionadas por la amplitud de presión esperada.

Durante mezcla y masterización, los niveles en dB SPL y las escalas logarítmicas tienen paralelismos con los niveles digitales (dBFS), aunque con diferentes referencias.

Procesado digital de señales (DSP)

En procesamiento digital (ecualización, compresión, limitación, normalización, análisis espectral), muchas operaciones descansan en magnitudes de amplitud o nivel (en dB).

Conclusión

Las magnitudes físicas del sonido — frecuencia, periodo, longitud de onda, amplitud (presión), intensidad, potencia, velocidad acústica, impedancia — son la base cuantitativa para describir y trabajar con ondas sonoras de modo riguroso.

Cuando un ingeniero de sonido o un técnico trabaja con micrófonos, sistemas de sonorización, mediciones acústicas o procesamiento digital, debe tener una comprensión clara de cómo estas magnitudes se relacionan entre sí, cómo varían con la distancia, el medio y cómo se representan en escalas logarítmicas (decibelios).

Gracias por tu lectura

RF